"97 percent of the scientists of the world [are] warning us about the devastating impact of global climate change if we don’t take action" - John Kerry
"The evidence is incontrovertible: Global warming is occurring." - American Physical Society
"the level of consensus [on climate science] correlates with expertise in climate science" - Consensus on consensus, Cook 2016.
Fundamentals of Science
What comes next in the sequence: 1, 2, 3, 4, 5?
The natural answer you might see on a typical IQ test would be 6, reasoning that the sequence represents the pattern of positive integers. However, if the pattern is “powers of primes”, then the next term should 7: 1,2,3,4,5,7. On the other hand, a graph theory aficionado might come to the “obvious conclusion” that the nth number in the sequence is “the number of disconnected 2-regular graphs on n vertices”, in which case the sequence continues with 8.
Indeed, it does not take much sophistication to realize that the next number in the sequence can be any number whatsoever. To see this, suppose we want the next number to be q. Then we build the function
𝑓(𝑥) = (𝑥−1) (𝑥−2) (𝑥−3) (𝑥−4) (𝑥−5) ((q-6)/120) + x
In this case, we have:
𝑓(1) = 0∗ (𝑞−6) + 1 = 1
𝑓(2) = 0∗ (𝑞−6) + 2 = 2
𝑓(3) = 0∗ (𝑞−6) + 3 = 3
𝑓(4) =0∗ (𝑞−6) + 4 = 4
𝑓(5) =0∗ (𝑞−6) + 5 = 5
𝑓(6) = 5∗4∗3∗2∗1∗ (q-6)/120 +6 = 𝑞
So, we can make the next number in the sequence be q=6, q=-100, or q= square root of -1. Indeed, we can similarly extend the original sequence by any collection of arbitrary numbers by replacing the (q-6)/120 term by an appropriate polynomial.
In effect, it is mathematically impossible to extrapolate the sequence 1,2,3,4,5 (or any other sequence) without external constraints. Still, despite a deficient understanding and modeling of our world, Science endeavors to perform just such a feat of extrapolation, with fantastic successes from airplanes to medicines.
To accomplish its goals, Science makes use of a number of understated and unsupported assumptions within the context of the Scientific method. The Scientist thus subordinates his worldview and decision-making to the fruits of these axioms, and he interprets any potentially falsifying evidence to the benefit of said axioms. When a Scientist refuses to acknowledge the inability of this process to make unequivocal statements about the world, he mirrors the Deist, the Ietsist, and the Atheist in establishing and following a religion of his own choosing.
A simpler example

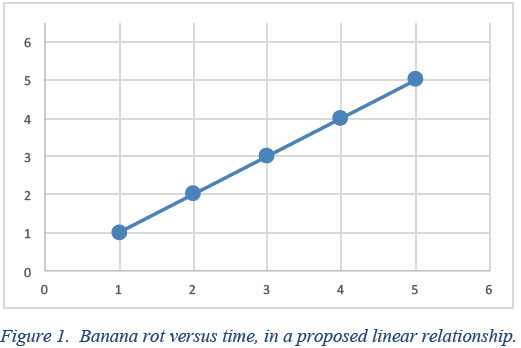
Consider, as a backdrop example, a highly simplified scientist measuring, say, the rot of a banana. Measuring the rot at regular time intervals, our simplified Scientist arrives at the first four measurements of our sequence (i.e., 1, 2, 3, 4 in some units of rot). Applying Occam’s razor as part of the scientific method, she might conjecture the simplest possible relationship between the measurements, that being a linear relationship, and hypothesize that the next measurement be 5 rot units (as in Figure 1). She would confirm this with a subsequent measurement and conclude with a theory: at the nth time, the banana will have rotted by n rot units.
If a colleague in a different lab measures banana rot for a longer period of time, and sees that the 6th measure is 7 rot units, rather than 6 as predicted by the theory, the Scientific method would demand that the theory be amended to account for the measurements 1,2,3,4,5,7, and, perhaps, the simplest explanation will become that the measurements are powers of primes.
As more colleagues independently confirm the first several measures of rot in their own experiments, without producing a counterexample, the modified theory will gain acceptance in the broader scientific community. In this manner, the Scientist would conclude that the theory best exemplifies the current state of knowledge about rotting bananas. Still, there are a number of strong assumptions in even this simplified example that bear further scrutiny.
Occam’s razor directs that an initial conjecture be the simplest explanation that fits the existing data, where simplicity is typically measured by the number of assumptions used. If the conjecture needs to be modified because of subsequent results, then, again, the simplest explanation that also fits the new data is chosen.
The key issue here, of course, is that choice of "simplest" is a subjective, since it is practically impossible to identify, much less enumerate, all the assumptions inherent in an explanation. Such assumptions may include the scientist’s past experiences, cognitive processing, chosen model and aesthetic tendencies. At the same time, as we saw earlier, there are literally an infinite range of hypotheses that will accurately fit any available data, both past and future.
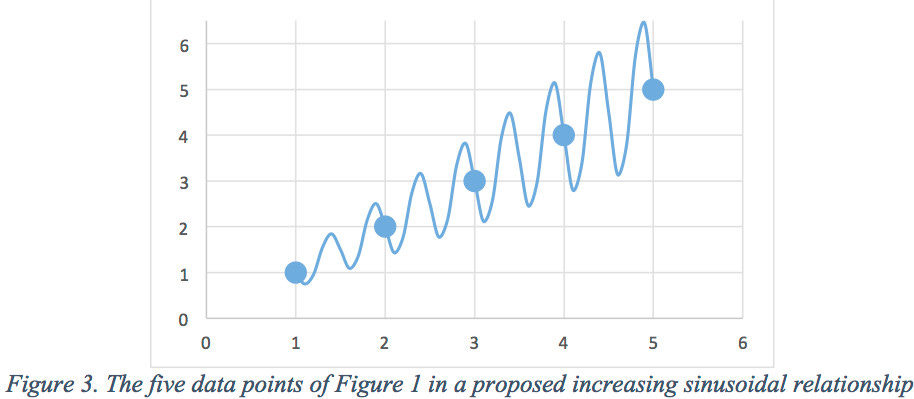
The putative line connecting our Scientist’s data in Figure 1 could easily represent a sinusoidal relationship (Figure 2) if there is a wave-like component, say due to diurnal temperature variations, or an increasing sinusoid (Figure 3) if there is feedback.
The Scientist might argue that the model of data points will change if, say, a sample point between times 1 and 2 confirms a sinusoidal behavior, but this will not resolve the mathematical cat-and-mouse game: no matter what data one provides, there are an infinite number of curves that exactly match all of the data and yet diverge from each other. Ultimately, the chosen relationship rests upon a number of subjective choices by the Scientist that drive the later analysis.
The Copernican Revolution
A legendary example of this tension is the battle of heliocentrism versus geocentrism that marked the Copernican revolution. The church insisted on a geocentric view of our solar system, in which the Earth is viewed as stationary with the other planets and Sun rotating around it. Copernicus insisted on the familiar heliocentric view that the sun is stationary and the planets rotate around it.
This great clash was, in fact, largely a political, rather than scientific, issue: one can accurately model the solar system within either reference frame. In the updated heliocentric model, the planets move (roughly) in ellipses around the sun. In the geocentric model, the sun and other planets move in curved paths around the Earth; these curves can be described analytically or as circles around circles around circles, etc. (so-called epicycles). In each case, a sense of infinite is needed to understand the trajectory of the various planets: a quadratic form with infinite domain for ellipses, and an infinite collection of circles for epicycles.
We prefer the Copernican view because we aesthetically like low-degree polynomials, but nature has no problems utilizing transcendental numbers like π or functions like sin(⋅), neither of which can be expressed precisely with a finite number of algebraic terms. As such, neither Copernicus nor the church can make a reasoned case that disqualifies the other.
Other assumptions of Science
Another cornerstone of Science is reproducibility: an experiment conducted under the same conditions at different times and places produces the same results. Of course, it is empirically impossible to recreate the same conditions in two different experiments, or, for that matter, to account for the different variables that affect them. Indeed, even a simplification such as the three-body problem admits no general analytic solution, and Heisenberg’s uncertainty principle makes it impossible for us to accurately measure, much less recreate, the conditions of an experiment.
There is yet another assumption inherent in reproducibility: that there is one universal truth and it does not change over time or space. This assumption is needed to preclude the possibility that different experiments will be measuring different truths (rather than supporting each other), though it may be challenged in statistical domains, most notably quantum mechanics or statistical thermodynamics, where repeated experiments necessarily produce different results and only aggregate statistics can be precisely characterized.
The assumption is also needed to preclude the possibility that the universe has changed between one experiment and its repetition, even though everything we experience in the world changes constantly: weather, people, ideals. Why should we insist that, somehow, the laws of the universe are the only constant and unmoving elements in our lives? Why should repeating the same experiment on two different ends of the universe produce the same result. Still, when we see a corner of space that is behaving differently from what we expect, we hypothesize not that the laws of the universe are different there, but that there is some unseen phenomenon, say a black hole or dark matter, that explain the anomalies.
In practice, experimenters selectively ignore errors they feel are unimportant, be they relativistic anomalies of Kepler’s ellipses or measurement anomalies of epicycle approximations. This disregard is at once essential, since there are too many sources of error to control, and also intuitive, in that we are not able to completely analyze the physics of the universe much less ascribe accurate error based on unknowable a priori models of error.
In essence, the Scientist subjectively guides the hypothesis, experiment, and analysis to reach a scientific conclusion, all the while having not just a vague understanding of the overall system, but even a vague understanding of just how vague this understanding might be. When other Scientists attempt to recreate the experiment, they start up front with the subjectivity of the original researcher. They may choose to either accept or reject the subjective choices, but this is a political, rather than evidentiary process.
Turtles all the way down

Unfortunately, the ability of science to impart the truth is even more dubious than what has been described thus far. Science rests upon a bedrock of mathematics – integrals, topology, differential equations, and the like, form the cornerstone of our understanding of mechanics and thermodynamics, biological processes and protein folding, even the electric circuits like those that run our cellphones. Indeed, we understand some scientific phenomena only second-hand through the lens of mathematics, including the “invisible” fields of gravity, electricity, and magnetism or the the wave-particles of quantum mechanics.
Yet, from the middle of the 20th century onward, mathematics is known to be without a firm foundation. Attempts to formalize set theory have experienced catastrophic collapse at the hands of a number of paradoxes, perhaps the most famous being Bertrand Russell’s paradox concerning the existence of a set of all sets. In a popular rendition, the paradox relates of a town in which the sole barber cuts only the hair of all residents who do not cut their own hair. The question then being whether the barber cuts his own hair (in which case he fails his own rule) or does not cut his own hair (in which case, by his own rule, he should).
Formalizing simple arithmetic failed just as spectacularly through the twin theorems of Kurt Gödel. The theorems roughly showed that axiomatic systems that contained arithmetic were either incomplete, meaning that they could not establish the truth of some statements within the system, or else inconsistent, meaning that they could prove some statement simultaneously true and false. We cannot prove that even arithmetic is consistent without resorting to additional axioms.
Going deeper into formalism, there is even question whether mathematical truth is singular or plural. For example, the axiom of choice, that we may choose a single entity from each of a (possibly infinite) collection of sets, has been shown to be independent of the consistency of Zermelo-Fraenkel set theory, which forms the foundation of mathematical logic. This means that one may freely assume or not assume this axiom without affecting the consistency of mathematics.
And yet, the abstract notion of infinity that is at the core of such antinomies is also essential to our experiences of the world. This is evident from the classical paradoxes of motion popularly attributed to the Greek philosopher Xeno, which cannot be resolved without an understanding of infinity.
The bottom line is that, in the words of the memoriable Morris Kline:
Mathematicians have been worshipping a golden calf – rigorous, universally acceptable proof, true in all possible worlds – in the belief that it was a God. They now realize it was a false god... There is reason to question reason.
Mathematics, the bedrock of Science, is itself on a shaky foundation with respect to its ability to project truth; at the same time, Science is shaped by the mathematics on which it is based.
Conclusion
Science rests upon a variety of assumptions that are neither supportable nor falsifiable, such as:
A singular, non-changing and uniformly applicable truth;
Reproducibility and repeatability of experiments in discerning this truth; and,
The ability of Occam’s razor to capture this truth through the lens of human subjectivity.
To the extent that climate scientists couch their findings in the language of "irrefutable" "incontrovertible" evidence or the support of their peers, they are expressing an unsubstantiated claim of religious faith.
Acknowledgments
The author gratefully acknowledges the feedback of David Berlove, Lazar Trachtenberg, and Aryeh Klapper on early versions of this work.